Unity 四元數的使用 - usage of Unity Quaternion
來聊聊四元數 (Quaternion),前陣子跟它搏鬥了一段時間,然後 … 恩 … 現在比較沒那麼困惑了。
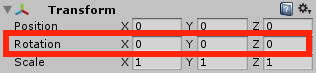
Unity 中常見的旋轉設定便是物件的 Rotation 屬性 (上圖),也就是以三個方向為軸的旋轉角。平時在編輯場景時操控旋轉相當直覺,可是當需要從 Script 中用程式碼去控制物件的旋轉時,這時候會發現原來 Rotation 屬性是由 Quaternion 這個類別來處理,身邊的許多人(包括我)雖然懂得利用一些 Unity Script 去旋轉物件,可是總是一知半解,對於複雜一點的旋轉操作沒有多少把握。於是努力去研究跟學習後,有了這篇初步的心得出現,拋磚引玉。
Unity 的旋轉 - 歐拉角 及 四元數
在 Unity 的場景編輯中,物件的旋轉是由三個角度來設定,使用上相當直覺,而這個定義旋轉的方式被稱為 歐拉角(Euler angles),詳細定義在 wiki 可以找到。在 Unity script 中,可以用 Transform.eulerAngles 來取得或設定物件的旋轉角度,不過歐拉角在先天上有些使用限制,例如 萬象鎖。以及因為三個角度的旋轉互相關聯而不獨立,不容易在 Unity script 進行複雜的處理,如果將兩個 歐拉角 進行相加的動作,並不一定會是想像中的組合結果,要取得兩個 歐拉角 之間的連續動作來完成動畫,也不是簡單運算便可以完成的。
同樣對應於物件的旋轉,利用 Transform.rotation 會取得 Quaternion 這個類別,稱為 四元數(Quaternion),是屬於代數領域中的一個存在,數學家發現它可以用來表示一個三維座標中的旋轉動作,而且具有相似於矩陣的特性,可以用來做連續旋轉的向量計算,後來廣泛應用於電腦科學中的 3D 繪圖。
Unity script 也提供 Quaternion 類別許多函式方便進行旋轉的運算,不過,Unity 中的 Quaternion 運算方式與代數領域中四元數的計算方式不完全相同,所以使用這個類別不需要知道四元數的詳細代數原理,知道相關原理與計算方式也不能直接套用於 Quaternion 類別的使用上。簡單來說,雖然定義相同,但完全不需要把 Unity 中的 Quaternion 類別當作一個代數來使用,它有自己的一套使用方式。
兩者比較:

Unity 中的四元數
雖然只是猜測,但我想 Unity 的四元數應該是用矩陣來實作,每當建立一個 Quaternion 類別時,它內部就會有一個 變換矩陣(Transformation matrix) 與之對應,用於將一個三維向量(Vector3 類別)變換(旋轉)成另一個三維向量,而這個旋轉的動作是相對的,可以應用任何三維向量之上,做出相同的旋轉動作;同時它也是可疊加的,對一個向量應用兩次四元數運算,就相當於旋轉了兩次,如果先將這兩個先進行相乘,再應用於同一個向量上,也會得到相同的旋轉結果。如果用矩陣乘法的角度來思考,Quaternion 類別的使用方式會容易許多。
1 | Quaternion rotation = Quaternion.Euler (0, 90, 0); |
上面是一個簡短的程式碼,因為四元數的參數比較難(數學不好),我利用 Quaternion.Euler(float, float, float) 這個函式來建立一個四元數,在此利用了歐拉角的易讀性,並為了方便運算,將旋轉的動作儲存為一個 Quaternion 類別,這個四元數所儲存的旋轉動作便是沿著 正y軸順時針旋轉90度,或稱 右轉。接下來分別用了三行程式碼對一個三維向量進行旋轉的動作,得到了 resultA、resultB、resultC 三個結果,進行四元數與向量的旋轉運算時,必須將四元數置於前方,就像使用變換矩陣與向量之間的乘法時,矩陣必須置於前方一樣。
起始的向量 Vector3.forward 中內含的值為 (0, 0, 1),這邊要注意 Unity 的三維坐標系是左手坐標系,也就是右側為X正向,上方為Y正向時,前方為Z正向。經過旋轉後:
- resultA 的值為 (1, 0, 0),也就是右轉了。
- resultB 的值為 (0, 0, -1),過程是進行了兩次的右轉,也就是成了向後轉。
- resultC 的值為 (0, 0, -1),與 resultB 的不同之處,這裡是先將兩個四元數相成為一個四元數後,在應用於向量上,結果與 resultB 相同,驗證了四元數的疊加性。
操作四元數時,幾個我常用的 Quaternion static 函式:
- Quaternion.Angle(Quaternion, Quaternion):取得兩個四元數之間的相對角度,也就是兩個旋轉動作之間的 “直線距離”,不知道如此比喻會不會比較好理解。
- Quaternion.Inverse(Quaternion ):取得四元數的反元素,也就是 “倒帶” 的動作,我通常會利用於修正項,後文會再次說明。
- Quaternion.Lerp(Quaternion, Quaternion, float):取得兩個四元數之間的補間動作,應用相當廣泛,自行控制物件的旋轉時往往會用到。
還有一個 non-static 函式 Quaternion.ToAngleAxis,用的不多,但對於操作四元數也是一個很必要的函式,可以取得旋轉動作的轉軸跟角度,原本這兩項資訊的取得需要透過代數運算,有了這個函式就真的不需要知道四元數的裡面到底如何運作了,此外這也是使用歐拉角時難以取得的資訊。
完整的函式內容請看 四元數的官方文件。
小範例:將陀螺儀變成你的遊戲控制器
Unity 有提供 API 取得裝置本身陀螺儀的資料,其回傳結果是 Quaternion 類別。剛剛提過,四元數表示的是一個相對的動作,不像向量有一個絕對的坐標系可以參考,所以照理說光是一個四元數是無法表達手持裝置目前的 “姿勢” 才對阿?實際上,手持裝置的陀螺儀預設了一個 “無旋轉的姿勢”,相對於這個預設的方位動作,用四元數表達了手機現在的陀螺儀狀態,不過這個預設值是不可知的,或者說是相當虛無的存在,進而使陀螺儀得回傳值也相當虛無 (不知道起點,所以有了過程也無法知道終點)。
為了將陀螺儀的資料變成我們可用的資訊,四元數的操作是必要的,我們用下面一個簡短的程式碼來說明。
1 | using UnityEngine; |
- Line12:啟動陀螺儀,雖說是啟動,但是預設的 “未旋轉” 跟這邊的啟動完全無關,未旋轉的狀態是內建於手持裝置的OS中的。
- Line14:取得當下的陀螺儀數據,這行程式碼運作於 Start() 中,所以就是儲存了腳本啟動當下的數值,當作解下來旋轉動作的原點。
- Line15:計算與儲存 _OriginGyro 反元素,將用於待會的坐標系修正上。
- Line16:嚴格上沒必要初始化,請將 _Pointer 想像成手持裝置後置盡頭所對準的方向,而現在啟動腳本的當下,以裝置鏡頭的角度假設了一個現實中的三維坐標系。舉例來說,如果你現在裝置鏡頭對準著你的正前方,那這個坐標系將會是:右手為正X方向,上方為正Y方向,前方為正Z方向。
接下來在 Update() 中取得每禎的陀螺儀數據,處理成可用於操控遊戲的資料,
- Line22:取得當下的陀螺儀數據。
- Line23:將陀螺儀的資訊用於旋轉 _Pointer。
- Line24:利用 Quaternion.Angle 這個 static 函式,取得 _CurrentGyro 與 _OriginGyro 之間的角度,這個角度是相對於在腳本啟動時,手機旋轉了多少角度。
- Line25:利用 _OriginGyroInverse 再次旋轉了 _Pointer,這次旋轉的目的是進行修正,讓 _Pointer 真正成為在假設的坐標系中,手持裝置後置鏡頭所對準的方向,原理下述。
回想一下在三維座標系中的經典問題:如果將原點移至 (10, 0, 0),那原本座標系上點的舊座標該如何修正為新的座標?答案是:將舊座標減去原點的變化量。
陀螺儀這邊我們應用了相同的邏輯,手持裝置預設了一個 “未旋轉” 的數據,也就表示它預設了一個座標系,一個方向不明的舊座標系。不過我們在腳本啟動時定義了自己的新座標系,同時儲存了當時的陀螺儀數據 _OriginGyro,現在新舊坐標系之間的變化量不是移動一段距離,而是旋轉的一個角度,_OriginGyro 便是這個旋轉變化量。
當 Line23 運算後的 _Pointer,因為單純是利用陀螺儀數據所旋轉得來的,它所包含的座標是使用了未旋轉的座標系(舊坐標系),但我們希望知道鏡頭在新座標系中的方向角度呀?所以我們在 Line25 將 _Pointer “減去” 了坐標系的變化量 _OriginGyro。不過,四元數是沒有加減的概念的,相對的正確動作是 “反過來旋轉”,也就是乘上四元數的反元素,這就是為什麼一開始我們需要計算 _OriginGyroInverse。
神奇的事發生了,在我們現實中假設的座標系上,我們現在不只得到了旋轉角度,連旋轉後的 “姿勢” 都有一個向量精確的標明出來。
後話
其實要取得手機的旋轉,還有個重力感傳器可以使用,而且相對簡單容易理解。但是,陀螺儀所包含的資訊更加全面多元,精確度也不會受到手機搖晃所影響,如果能夠學會它,當然要去使用呀!
另外現在 VR 相當的熱門,許多應用於 VR 的裝置使用四元數來作為回傳的旋轉數據,前陣子才有朋友為了修正 VR 裝置的感應器設置於不同角度時,得到的結果相當混亂而焦頭爛耳,最後放下對於歐拉角的堅持,利用四元數來修正便讓問題顯得相當容易。